Prilogenie

Осови точки №№ 24 и 53 (черт. 8^а) са поставени за притъпяване на върха на квартал 63. Оста 24-53 лежи само срещу един парцел и не се ползува за нищо: парцелът се определя от осите 22-24 и 22-53, поради което тези точки не се трасират на мястото.

Изоставят се на същите основания също така точките 140, 141, 142, 143 и 144 – (черт. 8^б), като вместо тях се трасира нова точка № 145, която напълно ги замества за нуждите на прилагането на плана.

2. ОСОВИ ЛИНИИ ПРИ НЕУСПОРЕДНИ РЕГУЛАЦИОННИ ЛИНИИ

Когато двете регулационни линии AB и CD на квартали №№ 16 и 54 не са успоредни (черт. 9), за удобство при даване на строителни линии се прекарват две оси, успоредни на двете регулационни линии на поменатите квартали.

3. ТРАСИРАНЕ С ПОМОЩНИ ОРДИНАТИ ПРИ ПРЕПЯТСТВИЯ

Трябва да се трасира осовата точка “а” (черт. 10) по оста 15-16 с ордината 8,70 м и абсциса 42,30 м от точка 16, в случай че ординатата минава през постройка.

По оста с начало точка 16 се отмерват абсцисите 40,30 и 44,30 м, т.е. с една и съща константа в случая 2 м, по-голяма и по-малка абсциса от отчетената по плана.

От получените точки се издигат помощни перпендикуляри със стойност, равна на отчетената, и се получават точките а₁ и а₂, разстоянието между които, като се разполови, дава търсената точка “а”.

Когато е невъзможно да се трасират еднакво дълги помощни перпендикуляри, отмерват се два различни по дължина перпендикуляри, така че средно аритметичната за тях да бъде отчетеният за точка “а”. В случая помощните перпендикуляри с 1,50 м в плюс и минус от тези за точка “а”. Полученото разстояние а₁ – а₂ също се разполовява и се намира мястото на точка “а” (черт. 11).

4. ТРАСИРАНЕ НА ПРАВИ УЛИЧНИ ОСИ С ПОВЕЧЕ ОТ ДВЕ ОСОВИ ТОЧКИ

При трасиране на прави улични оси с повече от две осови точки – междинни точки се спазва следното:

Когато началната и крайната осови точки се виждат една от друга, тогава изравняването на междинните осови точки става, като се центрира теодолитът на една от крайните точки и се насочва към втората, след което междинните осови точки се изравняват в линия с помощта на жалони, като се спазват междинните разстояния и положението на пресичащите се оси.

5. ТРАСИРАНЕ НА ПРАВИ УЛИЧНИ ОСИ ПРЕЗ ПРЕПЯТСТВИЯ

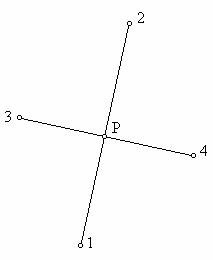
В случаи, когато оста минава по хълмист терен – (черт. 12) и от осова точка 1 не се вижда осова точка 4, а трябва да бъдат трасирани осови точки 2 и 3, които лежат на права линия с тях, се постъпва по следния начин:

Трасират се крайните точки 1 и 4 и се изчисляват координатите им от близки полигонови точки.

Изчислява се също посоченият ъгъл и разстоянието между тези точки. От разликата между посочените ъгли α_1,5 и α_1,4 се получава трасировъчният елемент – ъгъла β, с помощта на който и разстоянието 1-2, взето от карнета, се намира мястото (приблизително) на осова точка 2.

Поставя се теодолитът в тази точка, продължава се линията 1-2 по посока на осовата точка 4, отмерва се разстоянието 2-3, също взето от карнета и се получава приблизителното място на осова точка 3. По същия начин се постъпва и при станция 3, като при безгрешна работа, продължавайки правата 2-3, визурата трябва да премине през осова точка 4. В случай че се яви отклонение х, то се измерва и пропорционално на дължините 1-2, 1-3 и 1-4 се изчисляват съответните корекции за намиране окончателните места на точките 2 и 3, като се държи сметка и за положението на пресичаните оси 9-8 и 10-11.

За контрола се изчисляват координатите на пресечната точка с някоя полигонова линия, напр. точка Р. След това се изчисляват разстоянията 148-Р и 149-Р, с помощта на които се трасира върху терена точката Р и тя трябва да попадне върху оста 2-3; в противен случай работата се проверява.

Трасирането на междинните осови точки значително се опростява: ако между двете крайни точки има място, откъдето те се виждат (черт. 13).

В случая осова точка 1 и осова точка 4 не се виждат една от друга, понеже се намират от двете страни на едно възвишение. За да се трасира осова точка 3, която се намира на билото на това възвишение, се постъпва така:

Поставя се инструментът в точка 3′, лежаща приблизително в осовата линия 1-4, след това се измерва ъгълът (200-γ) при двете положения на тръбата. Отклонението q е равно на разстоянието от приблизителното място на осова точка (3) до действителното място (о.т.3′) и се изчислява по следната формула:

По груби данни мястото на точка 3′ се намира от регулационния план. Разстоянието D1 и D2 се отчитат също от регулационния план. Така изчисленото разстояние q се отмерва на терена от точка 3′ и се получава точка от уличната ос, около която трябва да бъде осовата точка 3. Нейното окончателно място се намира, като се отмери разстоянието о.т.1–о.т.3 или пък о.т.3-о.т.4 по уличната ос.

Прави се също така и ъглова проверка, като върху така определената осова точка 3 се измерва ъгълът, визирайки към осова точка 1 и осова точка 4, при двете положения на тръбата. Полученият ъгъл трябва да бъде 200^g. Допустимата ъглова разлика от 200^g е в зависимост от дължината на визурата, съответствуваща на 1 до 2 см отклонение от правата.

Трасирането на улична ос, ако крайните й точки не се виждат една от друга, може да стане и ако пред или зад тях в същата посока има височина, от която те се виждат. В такъв случай инструментът се поставя на височината по продължението на оста на улицата. Осовите точки в правата, определена от крайните точки, се трасират с помощта на теодолит Theo 030 или равноточен такъв.

6. ПРОДЪЛЖАВАНЕ НА ОСОВИ ЛИНИИ

Често пъти се налага продължаването на осови линии с инструмент. В случая се постъпва по следния начин:

Дадена е осовата линия, определена с осови точки 5 и 6 (черт. 14).

Необходимо е осовата линия също да бъде продължена на разстояние “b”, на края на което се определя точка “с”. За тази цел инструментът се центрира на осова точка 6 и се насочва тръбата към о.т. 5, след което се завърта на 200 гради, отмерва се разстоянието “b” по посока на визираната ос и се забива кол с₁. След това при второ положение на тръбата се завъртва алидадата и се насочва отново към осова точка 5. При повторно завъртване на тръбата на 200 гради се фиксира точка с₂. Чрез разполовяване на отсечката с₁ - с₂ се определя мястото на точка “с”, която вече лежи в продължението на осовата линия 5-6. Разстоянието “а” (о.т.5, о.т.6) трябва винаги да бъде по-голямо от разстоянието “b”, защото грешката от насочването расте в отношение b:a. Точките с₁ и с₂ съвпадат, ако в инструмента е отстранена колимационната грешка. Тя трябва да се отстрани преди започване на работата.

7. ТРАСИРАНЕ ОСНОВНИТЕ (ГЛАВНИ) ТОЧКИ ОТ КРЪГОВА КРИВА

За трасиране на основните (главни) точки от кръговата крива – начало, край и среда при даден радиус се постъпва по следния начин:

а. При достъпна пресечна точка на двете тангенти

Продължават се правите улични оси – тангенти до пресичането им в точка D, при която се измерва с теодолит ъгълът φ (черт. 15). Тогава

; .

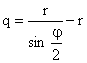От точката D по направление на двете прави улични оси се отмерва разстоянието Т и се получават точките “начало” и “край” на кривата, т.е. А и В. С помощта на ъгъла и разстоянието q се намира мястото на средата на кривата, т.е. точката S.

б. При недостъпна пресечна точка на двете тангенти

Когато пресечната точка на двете улици е недостъпна, тогава се избират точките D и Е, при които ъглите α и β и разстоянието “а” се измерват. Изчислението се извършва както в предидущия случай по формулите, означени на скицата (черт. 16).

Дадени: r и двете оси.

Избират се точките: D и Е, при което се измерват ъглите α и β и дължината “а”.

;

Трасират се от т. D: точката А с дължина DA=Т-b и точката F с дължина DF=T-b-t и от т. Е: точката В с дължина ЕВ=Т-с и точката G с дължина EG=T-c-t. Точката S се трасира, като се разполови отсечката FG.

Контрола: AF=FS=SG=GB=t.

8. ТРАСИРАНЕ ОСОВИ (ГЛАВНИ) ТОЧКИ ОТ КРЪГОВА КРИВА, КОГАТО ЕДНАТА УЛИЦА Е ТАНГЕНТА, А ДРУГАТА УЛИЦА Е СЕКУЩА КЪМ КРИВАТА

а. При достъпна пресечна точка “С” на тангента със секуща

Приема се точка “А” за дадена и трябва да се трасира точка “В” (черт. 17).

Измерват се ъгълът α и разстоянието “а”.

От двата правоъгълни триъгълника ACD и AED се изчисляват катетите им CD и AE, чиито хипотенузи са “а” за единия и “R” за другия триъгълник.

Пресечната точка “С” на правите улици е достъпна.

Дължината на тангентата се изчислява по формулата:

От т. “С” с изчислената дължина “Т” се определя точка “В”, която е начало на кривата.

б. При недостъпна пресечна точка “С” на тангента със секуща

Когато пресечната точка “С” на правите улици е недостъпна, избират се точките N и M (черт. 18).

Ъглите β и γ и разстоянията b и d се измерват.

Необходимите трасировъчни данни се изчисляват по формулите:

; ;

С определеното разстояние Т – е = МВ, от точка М се определя В, която е началото на кривата.

Пресечната точка “С” на правата улица е недостъпна.

;

Трасира се разстоянието Т-е с начална точка М.

9. ТРАСИРАНЕ НА КОШОВА КРИВА

Кошовата крива е комбинация най-малко от две или повече окръжности с различни радиуси, които тангират една след друга по непрекъснатата низходяща или възходяща степен на радиусите.

В регулационните планове при проектирането на главната улична мрежа, около уличните възли (кръстовища на две и повече нива) и при закръгляването на регулационната линия към кварталите, удобна за транспорта е кошовата крива. Тя е комбинация от две окръжности. В повечето случаи окръжността с по-малкия радиус е обхваната симетрично от двете си страни от по-голямата окръжност (черт. 19).

В тесен смисъл на думата окръжността с по-големия радиус трябва да се разглежда като преходна крива.

В практиката при регулационните планове тангентите на големите окръжности са по посока на осовите линии.

Когато са дадени тангентите, които сключват окръжностите, ще имаме:

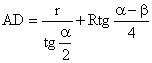В случай че тия тангенти са дадени всяка с по две точки, които определят точното направление на тия прави, ще може да се получат и съответните ъгли , , , , , както и техните пресечни точки А, В и D.

; .

При дадени тангенти имаме следните случаи:

а. Даден е единият радиус ; получаваме , като е дадено AD, ще получим и .

Ако е даден r, ще определим ;

б. Когато е дадена общата допирателна точка Т, ще имаме:

;

в. Когато е дадена точка К – върхът на кошовата крива, имаме:

;

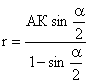
AK е известно, след това се получава:

;

10. ТРАСИРАНЕ НА КОШОВА КРИВА ОТ ДВЕ ОКРЪЖНОСТИ

За да не се получи деформиране на кошовата крива (черт. 20) в общата им точка Е (да имат обща тангента) поради изменението, макар и незначително на сключения между двете прави осови линии ъгъл при трасирането и поради неточното определяне началните точки А и В на кривата – приемаме за дадени само стойностите на двата радиуса R и r и тангентната стойност AC=a на окръжността с по-голям радиус, а другата тангентна стойност се определя по формулата .

Ъгълът β се измерва с теодолит на място.

За намиране тангентите t₁ и t₂ изчисляваме най-напред централните ъгли α₁ и α₂ по формулите: ; , след което изчисляваме: ; и .

Точката В се трасира от върха С с изчислената дължина СВ=b. Точките M и N се трасират съответно от точките А и В с изчислените тангенти t₁ и t₂, а след тях и точката Е, изхождайки от М и N (черт. 20).

11. ТРАСИРАНЕ ПРЕСЕЧНА ТОЧКА НА ОКРЪЖНОСТ С ПРАВА ЛИНИЯ

Дадени са направленията на правите улици, минаващи през точките А, Б, В и радиусът на улицата в крива (черт. 21).

Търсят се трасировъчните елементи за точка Б, тъй като тези за точките А и В се намират съгласно черт. 15 или 16 и най-напред се трасират.

Продължава се правата, която минава през Б, до пресичането й с една от тангентите и се измерва ъгълът β. В случай че това е невъзможно, ъгълът β се намира съгласно черт. 17. Измерва се разстоянието NB=t или MN.

След това по формулата: се изчислява разстоянието х. С помощта на същото (х) и ъгъла β се трасира точка Б.

12. ТРАСИРАНЕ ПРЕСЕЧНА ТОЧКА НА ДВЕ ОКРЪЖНОСТИ

Дадени са радиусите r и R на двете окръжности и координатите на точките А, С и В. Точките А и В са началата на двете криви (черт. 22).

От координатите на А и В се изчисляват координатите на центрите О₁ и О₂ по познатата формула:

1. ; .

2. ; .

От получените координати на центровете О₁ и О₂ на окръжностите се получава разстоянието “С” между двата центъра:

и посоченият ъгъл:

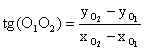Чрез страните на триъгълника МО₂О₁ се изчисляват ъглите му α, β и γ по формулите: ; ; ; където: .

Изчисляват се посочените ъгли на отсечките О₁М и О₂М

;

Координатите на пресечната точка М на двете окръжности се изчисляват двукратно от двата центъра на окръжностите О₁ и О₂, а именно:

- от точка О₁

;

- и втори път от точка О₂

;

Получените два чифта координати за точка М трябва да бъдат еднакви.

С координатите на точките А, С и М и втори път с координатите на точките В, С и М се изчисляват два чифта координати съответно (х₁ и у₁) и (х₂ и у₂) на точката М по отношение на осовите линии СА и СВ.

Изчислението на координатите х и у на точка М по отношение на осовите линии СА и СВ става бързо с помощта на таблица за квадратите на числата или с електронен калкулатор по формулите:

;

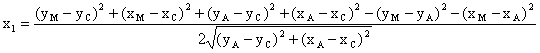
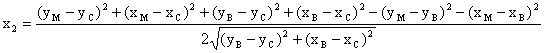С помощта на тези два чифта координати (х₁ и у₁) и (х₂ и у₂) се трасира двукратно точката М един път спрямо правата АС, другия път – спрямо правата АВ.

13. ТРАСИРАНЕ НА ПОДЗЕМНИ ГАЛЕРИИ, ТУНЕЛИ И ДРУГИ

При трасирането на обектите по подземното строителство се определят подземните посоки на началната и крайната точки и наклоните. Трябва да се подчертае, че при подземното трасиране точността на подземните дължини има по-малко значение, отколкото тази за посоките и денивелетните разлики.

Ако определянето на координатите на установените точки А, В, С и D (черт. 23) не може направо да се извърши, то за целта според местните условия и големината на обекта, между точките В и С се поставя, измерва и изчислява полигон или триангулация. Броят на избраните полигонови точки по възможност да бъде малък поради неблагоприятното натрупване на грешки вследствие на тежки теренни условия.

В случай че точките В и С са началната и крайната точки на един тунел (черт. 23) и АВ и CD са установени посоки, от координатите на точките А, В, С и D могат да се изчислят ъглите α, β и γ като разлики от посочените ъгли.

След като се изчислят страните ВС (от координатите), ВР и СР (по синусовото правило), тангентите МР и PN (от дадения радиус и ъгъл γ) съгласно черт. 15, то по дадените посоки АВ и DC и изчислените разстояния ВМ=ВР-МР; CN=CP-NP от точките В и С, се определят началната точка М и крайната – N на кривата.

Подобните точки от кривата се трасират чрез перифериални ъгли (черт. 26).

14. ТРАСИРАНЕ ПОДРОБНИ ТОЧКИ ОТ КРЪГОВА КРИВА

За да се получат подробни точки от самата крива, била тя осова, или регулационна линия, се прилагат различни методи в зависимост от особеностите на терена и препятствията, които се срещат на мястото. За да се трасират подробни точки от кръговата крива, която е установена със своите елементи върху терена и е с определен радиус, се прилагат следните методи:

а) правоъгълни координати;

б) перифериални ъгли;

в) последователни хорди.

а. Трасиране чрез правоъгълни координати

При този начин във връзка с известни данни за терена, препятствия от съществуващите сгради и други естествени теренни особености за трасиране на кръговата крива се използват обикновено два метода: чрез тангентата и чрез хордата.

Трасиране чрез тангентата

Този метод се използува в незастроени терени, където може да се продължат правите отсечки на улични оси, които се явяват тангенти в точка А – начало и В – край на кривата.

Тангентата AD се приема за абсцисна ос, от която се издигат перпендикуляри, чиито краища определят точки от кръговата крива (черт. 24).

За да се определят точки от кръговата крива, например 1, 2, 3 и т.н., трябва да се знаят абсцисите х₁, х₂, х₃ и ординатите у₁, у₂, у₃, които се изчисляват аналитично. От чертежа се вижда, че у1 = А - 1′, но понеже А1′ = АО - О1′ = R - 1′О; то триъгълниците О1′1 се получава, че О1′ = Rcosα, следователно ; .

Когато се дават определени значения на α, съответно се изчисляват стойностите х и у.

В практиката кръговите криви се разбиват обикновено не чрез даване на ъгли, а на равни ъгли, по които се изчисляват съответните ъгли по формулите:

; ; и т.н.

Друга формула е , в която за х се дават подходящи значения и се добиват ординатите у.

Съществуват специални таблици за разбиване на криви, в които величините х и у са дадени за различни радиуси и дължини на дъгите.

Препоръчва се в случая да се използуват таблиците за разбиване на кръгови криви от авторите Феодор и Въжеенски.

Трасиране чрез хорда

Често пъти по теренни причини или поради застрояване е по-изгодно трасирането да стане по хордата АВ, като се излиза от двете страни на точката , която е пресечната на радиуса през точка S “среда крива” и самата хорда. Тази точка се намира, като се раздели хордата на две половини, така че . За да се трасира част от окръжността чрез хордата АВ, необходими са абсцисите ; ; и ординатите ; ; ; и т.н. (черт. 25). С други думи, за да се трасира кръговата крива, изхождайки от хордата, абсцисите се изчисляват, както тези при разбиване кръговата крива по тангентите, а ординатите се изчисляват като разлика между стрелата и съответните ординати към тангентата у₁, у₂, у₃ и т.н. Дължината на перпендикуляра (стрелата) се изчислява по формулата:

Друга формула е 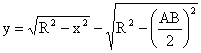, в която се дават подходящи значения на х, съответно се намират стойностите на у.

Предимствата на начина за трасиране кръгови криви с координати се състои в това, че всяка точка от кривата се определя независимо от останалите, вследствие на което е изключено предаването на грешки при трасирането на следващите точки.

При трасирането на дъгови криви с координати се използуват таблица, призма и ролетка, докато при случаите, които ще бъдат изложени по-долу, е необходимо трасировачът да разполага и с ъгломерни инструменти. Поради изтъкнатите предимства, горните начини са най-използуваните.

б. Трасиране чрез перифериални ъгли

Този метод се използува там, където трябва да се трасира улична ос между застроени вече квартали (черт. 26).

За случая се постъпва така:

Центрира се инструментът върху точка А, която представлява началото на кривата, и се отмерва предварително изчисленият ъгъл α, заключен между продължението на правата ос, която се явява и тангента в точката А. Изчисленият ъгъл трябва да отговаря на хорда S, която е предварително избрана – обикновено 10 м. Същата се отмерва по дясното рамо на отмерения ъгъл. Така се получава точка 1, която лежи върху кръговата крива. След това се отмерва ъгълът 2α и от получената точка 1, опъвайки ролетката с дължина 10 м, се намира мястото на точка 2, така че тя да попадне в дясната визура на отмерения ъгъл 2α. След това се отмерва 3α и разстоянието от преди това получената точка 2, пак 10 м, така че краят на ролетката с означение 10 м да попадне във визурата на отмерения ъгъл 3α. Така се продължава с ъгъл 4α, като по същия начин се получава точка 4, която лежи на кръговата крива. Ъгълът се изчислява по формулата: , като S се приема на 10-15 или 20 метра. Ако линията на визирането – например А-4, се получи доста дълга, което ще наложи допускането на някои грешки или пък визирането ще срещне някое препятствие, в такъв случай инструментът се пренася от точка А в точка 4, която е и последната трасирана точка на окръжността. В точка 4 се определя тангентата, която се получава, като по посока А-4, предварително сигнализирана, се отмери ъгълът 4α така, както е означено на скицата.

От така определената посока на тангентата Е4 в точка 4 се отмерва ъгълът α и по новата визура се отмерва разстоянието S, прието вече по-горе и се получава точка 5. По-нататък се отмерва отново ъгъл 2α и от точка 5 с дължина на ролетката, например 10 м, се гледа краят на ролетката да попадне във визурата 2α. С изпълнението на това условие се получава точка 6. Ако е необходимо, по същия начин се продължава и по-нататък за получаване на нови точки.

в. Трасиране чрез последователни хорди

Трасирането чрез последователни хорди се използува, когато по двете страни на трасираната улица има препятствия и оста на улицата трябва да минава в средата на един пояс с ширина на улицата, който предварително да бъде добре разчистен.

Например:

Дадена е тангентата А-Т и радиусът на кръговата крива.

Да се трасира чрез последователни хорди дадената крива. Приема се дължината на хордата да е равна на 10 или 20 метра. С така приетата S = 20 м (черт. 27) се изчислява ъгълът α по формулата:

Първата точка 1 от кръговата крива се трасира с помощта на координатите х и у, ; .

С така получените координати, като се излиза от тангентата λ-Т, се получава точка 1; за контрола се измерва разстоянието А – 1, което трябва да бъде равно на дължината на хордата S=20 м. По-нататък се постъпва така:

Продължава се хордата А – 1, като по направлението й се нанася величината S=20 м, и се получава точка 2′. От чертежа е ясно, че ако се опише дъга с лентата около точка 1, тогава на разстояние d надясно от точка 2′ ще се получи втора точка 2 от кръговата крива. Следователно, въпросът се свежда към намиране големината на разстоянието за дадените хорда S=20 м и радиус R. От подобието на триъгълниците 1, 2′, 2 и 0, 1, 2 следва, че , откъдето . След трасирането на точка 2 от кръговата крива се продължава хордата 1-2 на дължина S=20 м и се получава точка 3′. Като се държи ролетката неподвижна в точка 2, краят й се движи в дясна посока на разстояние d от точка 3′ и се получава мястото на новата точка 3 в кръговата крива. По същия начин се постъпва за точка 4 и т.н. Този начин е много удобен, защото се използува само ролетка. Той има обаче това неудобство, че грешките, допуснати в една предидуща точка, се предават последователно на следващите точки.

15. ТРАСИРАНЕ НА ЕЛИПСА

В плановото изграждане на населените места, елипсата много често се приема за очертаване на хиподруми, колодруми, градини, паркове и други. Елипса се нарича геометрическото място на точки, чийто сбор на разстоянията от две дадени точки Р₁ и Р₂, наречени фокуси, е постоянна величина. Елипсата се изразява чрез формулата: , където “а” е голямата, а “b” – малката й полуос.

Най-простият и разпространен начин за разбиване на елипса се състои в следното:

Дадени са полуосите на елипсата “а” и “b” (черт. 28).

С център “О” се трасират две окръжности, едната с радиус “а” на голямата полуос на елипсата, а другата с радиус “b” на малката полуос на елипсата. След това от центъра “О” се трасират няколко направления: О-1′, О-2′, О-3′ и т.н., пресичанията на които с двете окръжности дават съответно точките 1′, 2′, 3′, 1″, 2″, 3″ и т.н., от точките 1′, 2′, 3′ се прокарват успоредни линии на оста “Х”, която съвпада с малката полуос и през точките 1″, 2″, 3″ - линии, паралелни на оста “у”, съвпадаща с голямата полуос на елипсата. Пресечните на тези линии определят местата на точките 1, 2, 3, които са точки на елипсата.

16. ТРАСИРАНЕ НА СПОМАГАТЕЛНИ ОСОВИ ТОЧКИ ПРИ ТРАЙНИ ПРЕПЯТСТВИЯ

Спомагателните осови точки се трасират след окончателно установяване местата на крайните точки на оста, която минава през трайни препятствия. Примери:

Трябва да се трасират спомагателните осови точки 1, 2, 3 и 4 по оста АВ (черт. 29). Поставят се видими един от друг сигнали на правата M-N, която се избира успоредно на оста на разстояние “а”, желателно по-малко от 20 м, за да може да се отмери с 20-метрова ролетка. От желаните разстояния: х₁, х₂, х₃ и х₄ се издигат перпендикуляри с дължина, равна на “а”. Краищата на перпендикулярите определят местата на търсените точки – 1, 2, 3 и 4.

Ако е невъзможно да се прекара успоредна линия на оста, избира се правата МВ, към която от точка А се спуска перпендикуляр (черт. 30), разстоянията от петата на перпендикуляра до т.т. А и В се измерват (у и х). На подходящи разстояния х₁, х₂, х₃ и х₄ се издигат перпендикуляри, чиито стойности се изчисляват по формулите:

; и т.н.

Чрез изчислените ординати се определят местата на търсените точки 1, 2, 3 и 4.

Когато горните начини са неприложими, избира се произволната права MN (черт. 31), към която от А и В се спускат перпендикуляри, чиито дължини “а” и “b” и разстоянието между тях “х” се измерват. На желаните разстояния по правите MN – х₁, х₂, х₃ и х₄ се издигат перпендикулярите (y_n+a) с дължини, получени по формулите, дадени по-горе.

За да се трасират междинните осови точки “а” и “b” от оста А-В се избира полигоновата точка С (черт. 32). Измерват се двукратно дължините АС и ВС и ъгълът при точка С “γ”.

Тогава: , а от формулата , откъдето .

Събирайки стойностите на получените p и q, се получава ъгълът α, а от разликата им – ъгълът β.

Теодолитът се поставя последователно в точки А и В и се отмерват съответно ъглите α и β, като се започва от точка С, по отмерените посоки се фиксират съответно точките “а” и “b”. Местата на точките А, В и С се избират така, че да може по тях да се измерват ъглите и дължините АС и ВС, а така също и да бъдат възможно най-близко до постройката или препятствието.

Избират се полигоновите точки С и D и се измерват ъглите α, β, γ и δ и дължините от А и В съответно до С и D (черт. 33). С помощта на тези данни се изчисляват координатите на точките А, В, С и D в произволна система. Изчисляват се координатите на “b” и “с” като малки точки с разстояния, взети от плана. От така получените координати се изчисляват трасировъчните елементи за точка “b” (m и n), за точка “с” (p и q) и за точките “а” и “d” съответно φ и ψ. Точките “b” и “с” се намират, като се засекат с ролетка от фиксираните “С” и “D”, изчислените m, n, p, q, а точките “а” и “d” се трасират като в предния пример. Разстоянието (b-c) се измерва и се сравнява с изчисленото – за контрола (черт. 33).

Когато е невъзможно да се получават благоприятни засечки за намиране на местата на “b” и “с” при предния пример, тогава се поставят повече полигонови точки, например: C, D, E и F и се постъпва както в предния пример (черт. 34).

За точките “а” и “d” могат да се получат повече трасировъчни данни, например не само ъглите φ и ψ, но още и разстоянията от “а” до F и С и от “d” до Е и D, а за точките “b” и “с” в повече трасировъчните разстояния до точките “m” и “n”, като координатите на последните се получават както тези на малки точки по съответните полигонови линии, разстоянията до тях (F-m) и (D-n) се вземат така, че да се получат добри засечки при “b” и “с”, а “m” и “n” се трасират по правите на същите разстояния, които са изчислени.

17. НАЧИН ЗА ИЗБЯГВАНЕ НА КЪСИТЕ СТРАНИ ПРИ КООРДИНИРАНЕТО

При изчисляване координатите на осовите точки късите страни се избягват, като се имат предвид следните примери:

а) Осови точки 28 и 29 (черт. 35^а) са много близо една до друга и при ъгломеренето се получават недопустими ъглови грешки. За избягване на такива грешки от станциите 27 и 30 се визира както към 28, така и към 29. От станция 28 се визира към 27, 30 и 47, а от 29 съответно – към 27, 30 и 21.

По този начин осовите точки 28 и 29 могат да се изчислят в две самостоятелни вериги: например, верига с точки 27, 28 и 30 и тази с точки 27, 29 и 30, като страните 27-29 и 28-30 ще представляват сбора от тези между 27-28 и 28-29, респективно 28-29 и 29-30.

В случай че при осова точка 29 има чупка (черт. 35^б), то се образуват веригите 27-29-30 и 27-28-47.

В случай че разстоянието 28-47 е късо (черт. 35^в), образуват се веригите 27-29-30 и 27-28-30, като по този начин се измерва допълнителната страна 28-30.

18. СВЪРЗВАНЕ С НЕДОСТЪПНА ТРИАНГУЛАЧНА ТОЧКA

Свързването на осовата мрежа с триангулачната мрежа става, като се визира от триангулачната точка към определените осови точки и най-малко към две триангулачни точки. Когато триангулачната точка е недостъпна (например камбанария, кула, гръмоотвод и др.), свързването става по следния начин:

Избира се подходящ триъгълник, т.е. по възможност равностранен, или когато това е невъзможно, то отношението на страните му да не бъде по-малко от 1:3.

От осовите точки 1 и 2 (черт. 36) се визира към недостъпната триангулачна точка Р и от едната от тях, например от точка 2 се визира и към триангулачната точка Р₁, измерват се ъглите α, β, ε и страната с. Страните а и b се изчисляват по синусовото правило, а страната РР₁ се изчислява от координатите на триангулачните точки. Изчислява се и посочният ъгъл РР₁ от координатите на точките, а от триъгълника 2РР₁ (пак по синусовото правило) – ъгъл δ, откъдето се намира ъгълът φ. Към посочния ъгъл РР₁ се прибавя ъгъл φ и се получава посочният ъгъл на страната Р-2. Към този посочен ъгъл, като се прибави ъгълът γ, се получава посочният ъгъл на страната Р-1. Ако от осовите точки не се вижда друга триангулачна точка, или фигурата не е подходяща, трябва да се избере нова спомагателна точка, свързана с осовата мрежа, от която да се виждат освен недостъпната още и една друга триангулачна точка.

19. ИЗЧИСЛЯВАНЕ КООРДИНАТИТЕ НА ПРЕСЕЧНАТА ТОЧКА НА ДВЕ ПРАВИ, ДАДЕНИ С КООРДИНАТИТЕ НА КРАЙНИТЕ СИ ТОЧКИ

Когато са дадени координатите на точките 1, 2, 3 и 4 и се търсят координатите на пресечната точка Р, използуват се формулите, обобщени в приложения формуляр (черт. 37).

В редове 1, 2, 5, 6 и 12 (за ред 12 само на лявата страна) се вписват координатите на дадените точки. След това се образуват разликите между тях, съответно и редове 3, 7 и 8 (за ред 8 само от дясната страна). Като се разделят разликите, се получава и , което се записва в четвъртия и осмия ред на лявата половина на формуляра.

Попълват се редове 9 и 10 (в дясната половина на формуляра) и след това, чрез алгебричен сбор на редове 8, 9 и 10 от дясната половина се получава сумата (∑) в ред 11. В ред 12 в дясната половина се получава разликата К₁-К₂, след което се разделя сумата (∑) от ред 11 на разликата К₁-К₂ от ред 12 и се попълва абсцисата Х на точка Р в ред 13 (от дясно на формуляра). След това се преминава в лявата част на формуляра, където в редове 10 и 11 се вписват означените стойности, след което, като се съберат алгебрически редове 10, 11 и 12, получава се ординатата у на точка Р, която се записва в ред 13.

Пресечна точка на две прави

+ 22 355,87

+ 52 896,66

+ 22 307,17

+ 52 655,47

+ 48,70

+ 241,19

+ 0,20 192

+ 0,20 194

контрола

+ 22 446,27

+ 52 818,48

+ 22 293,14

+ 52 842,78

+ 153,13

- 24,30

- 6,30 165

- 14,03

- 6,30 067

контрола

+ 332 996,70

ý +

Контрола:

10.

- 10 632,19

+ 10 632,19

11.

+ 10 668,40

+ 343 614,86

ý :

12.

+ 22 307,17

+ 6 503,57

13.

+ 22 343,38

+ 52 834,81

14.

+ 12,49

+ 61,85

15.

+ 102,89

- 16,33

Черт. 37

За контрола на изчислението съответните разлики се вписват в редовете 14 и 15. Като се разделят и се получават К₁ и К₂, които се вписват съответно в графа 4 (от дясната половина за графа К₁) и графа 9 (от лявата половина за К₂). Стойностите на К₁ и К₂ трябва да бъдат същите, каквито са по-рано получени, с малки разлики, произлизащи от закръгляването.

Произведенията К₁.Х₁ и К₂.Х₃ се записват с обратни знаци, както е показано на лявата половина в ред 10 и на дясната половина в ред 9 на формуляра.

При всички действия във формуляра да се обръща внимание на алгебричните знаци.

20. ИЗЧИСЛЯВАНЕ НА ОТСТЪПКИТЕ ПРИ ПРЕСИЧАНЕ НА ПРАВИ ОСИ

Отстъпките се изчисляват с помощта на таблици за естествените стойности на ъгловите функции и сметачна машина или със специални таблици, съставени за тази цел, където стойностите на отстъпките се получават направо от таблицата. Изчислението с такива таблици се подрежда и извършва в регистър (Приложение № 10) и съобразно посочените там формули. Едновременно с това в същия регистър се извършва и контролът на получените отстъпки.

По-големи подробности за начина на работата с таблиците, определяне знаците на отстъпките и пр. са дадени в упътването към самата таблица.

При определяне знаците на отстъпките трябва да се обърне особено внимание, като се има предвид следното:

а. За ъгли α на пресичането на улиците (при върха на квартала) от 0 до 100^g, т.е. в I квадрант отстъпките са винаги положителни.

б. За ъгли на пресичането на улиците от 100^g до 300^g, т.е. във II и III квадранти, знаците на отстъпките зависят от големината на ъгъла, големината на полуширините на улиците и тяхната взаимна комбинация за всеки отделен случай. Следователно при определяне знаците на ъгли във II и III квадрант трябва да се обърне най-голямо внимание; тук те могат да бъдат както положителни, така и отрицателни.

За ъгли от 300^g до 400^g, т.е. в IV квадрант, отстъпките са винаги отрицателни.

Положителните отстъпки се нанасят от осовата точка по направление на оста към квартала, а отрицателните отстъпки се нанасят по обратна посока, по продължение на оста на улицата.

По този начин се изчисляват отстъпките на всички видове пресичания на прави улични оси с различни широчини на улиците.

На всеки хоризонтален ред от регистъра се изчисляват по един чифт отстъпки (за една регулационна чупка).

Започва се с отстъпката на квартала с най-малък номер, като след изчислението им се оставя един празен ред и тогава се продължава изчисляването на отстъпката на квартала със следващия пореден номер.

Отстъпките могат да бъдат изчислени с електронноизчислителна машина, за което има съответни специални програми.

21. ИЗЧИСЛЯВАНЕ НА ОТСТЪПКИТЕ ПРИ ОСИ, КОИТО СА ЧАСТИ ОТ ОКРЪЖНОСТ

Правата осова линия е тангента към кривата

Когато правата осова линия е тангента към кръгова осова линия, тогава отстъпката е равна на нула (черт. 38).

Правата осова линия не е тангента към кривата

Когато правата (осова) линия не е тангента на кривите (черт. 39^а, 39^б, 40^а и 40^б), изчисляването се извършва по приложения регистър (Приложение № 11). В първата графа на регистъра се вписва номерът на квартала, а под него – номерът на осовата точка.

Във втората графа се отбелязва стойността на половината от ширината на улицата с праволинейна ос, а под нея – тази на улицата в “крива”.

В третата графа се вписва половината от стойността на хордата, а под нея – стойността на радиуса.

В четвъртата графа се отбелязва стойността на ъгъла α, който е пряко измерен и стойността , изчислен по формулата: , където АВ е измерената страна.

В следващите четири графи се изчислява ъгълът γ по формулите: при изпъкнала крива; при вдлъбната крива.

В петата графа се записва ъгълът β и се записва разликата или сумата на ъглите , съответно за квартал с изпъкнала или вдлъбната крива.

В шеста графа се записват стойностите и .

Кривата осова линия е изпъкнала по отношение на квартала

а) Центърът на кривата е вътре в квартала (ъгъл γ е положителен)

; ; ; ; ;

б) Центърът на кривата е извън квартала (ъгъл γ е отрицателен)

; ; ; ;

Кривата осова линия е вдлъбната по отношение на квартала

а) Центърът на кривата е вътре в квартала (ъгъл γ е положителен)

; ; ; ; ;

б) Центърът на кривата е извън квартала (ъгъл γ е отрицателен)

; ; ; ;

В графа седма се записва разликата и разликата или сумата съответно за изпъкнала и вдлъбната крива.

В графа осма се записват стойностите на и γ. Когато ъгълът γ се получи отрицателен, това означава, че центърът на окръжността се намира извън квартала, а когато е положителен – центърът се намира в квартала.

В следващите три графи се изчислява отстъпката а′ по формулите: при изпъкнала крива; при вдлъбната крива.

В графа девета се записват стойностите и . Знаците “минус” са при изпъкнала крива, а знаците “плюс” са за вдлъбнатата крива.

В графа 10 се записват стойностите и . Знаците са също както в графа 9.

В графа 11 се записва стойността а′, получена чрез алгебричния сбор на изразите от графите 9 и 10. Тя може да бъде положителна или отрицателна.

В следващите графи се изчислява b_p по формулите: при изпъкнала крива; при вдлъбната крива.

В графа 11 се записва стойността .

В графа 12 се записва разликата или сумата съответно за изпъкнала и вдлъбната крива и стойността на израза: .

Знакът “плюс” е за изпъкнала крива и знакът “минус” – за вдлъбната крива.

В графа 13 се записва стойността . Знакът “минус” е за изпъкнала крива и знакът “плюс” – за вдлъбната крива и изразът , където знаците пред “b” и “γ” са “минус” при изпъкнала крива и “плюс” при вдлъбната крива.

В графа 14 се записва стойността b_p, получена чрез алгебричен сбор на изразите от графи 12 и 13.

Изчислява се b′ по формулите: при изпъкнала крива; при вдлъбната крива.

В графа 14 се записва стойността косинус на разликата или сбора , разликата при изпъкнала крива и сборът при вдлъбната крива.

В графа 15 се записва стойността на израза , където знаците “минус” са при изпъкнали криви и знаците “плюс” при вдлъбнати криви. Записва се стойността b′, получена чрез алгебричен сбор на изразите от графи 3 и 15. Стойността b′ може да се получи положителна или отрицателна.

За контролиране на работата по формулата в графата “забележка” се записват и сравняват сумите , които при вярна работа непременно трябва да са еднакви. В противен случай изчисленията се повтарят.

Пресичане на две кръгови осови линии

Дадени са координатите на точките А, В и С (където точка А е пресечната точка на двете оси, а точките В и С са съседните осови точки от кривите), радиусите на кривите R₁ и R₂, полуширините на улиците a и b и ъгълът α (черт. 41, 42 и 43).

От координатите на точките А, В и С изчисляваме страните АВ и АС. Ъглите β и δ изчисляваме по формулите:

Изчисляваме ъгълът φ (при центъра О₁ на окръжността К₁ между правата, успоредна на страната АС и правата, свързваща двата центъра) по формулата: .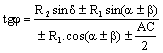

С помощта на ъгъла φ изчисляваме разстоянието “с” между центровете на двете окръжности.

С помощта на изчисленото разстояние “с” и известните “f” и “d” (където и ) изчисляваме ъгъла ψ.

, където .

С така изчислените ъгли ψ и φ и ъгъла α изчисляваме ъглите γ₁ и γ₂, а след това и самите отстъпки b_p, b′, a_p и а′

Кривите изпъкнали по отношение на квартала

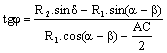; ; ; ; , където ; ; ; ; ; ; ; ; ;

Кривите вдлъбната и изпъкнала по отношение на квартала

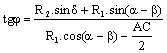; ; ; ; , където ; ; ; ; ; ; ; ; ;

Кривите вдлъбнати по отношение на квартала

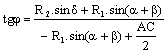; ; ; ; , където ; ; ; ; ; ; ; ; ;

За контрола се изчислява два пъти дължината S.

Допуска се разликата между двете стойности да не бъде по-голяма от 2 см. В противен случай изчисленията се повтарят.

22. ИЗЧИСЛЯВАНЕ КООРДИНАТИТЕ НА ВЪРХОВЕТЕ НА КВАРТАЛИТЕ

Координатите на върха А′ на квартала се изчисляват двукратно за контрола – един път по отношение на оста АВ и втори път по отношение на оста АС с абсциси – полуширините на улиците “а” и “b” и ординати отстъпките а′ и b′. За изходно начало служи осовата точка А с координатите си (черт. 44).

За целта най-напред се изчисляват координатите на точките М и N – петите на перпендикулярите, спуснати от точка А′, както следва:

От черт. 44 имаме: ; .

От подобието на триъгълниците АММ′ и АBD имаме: ; , където: ; ; където: .

От подобието на триъгълниците ABD и A′ME имаме: ; ; ; .

След което получаваме: ; .

Величините и се вземат готови от координатните изчисления на осовата мрежа за съответния посочен ъгъл α на страната АВ.

Аналогично получаваме координатите на точка А′ втори път чрез оста АС: ; , където: ; са стойностите на синуса и косинуса на посочения ъгъл по оста АС.

Във формулите за и знаците на членовете, в които участвуват величините а′ и b′, зависят от това в кой квадрант са посочните ъгли на отсечките АМ и MN или се вземат от самите координатни изчисления на осовата мрежа, а знаците на членовете, в които участвуват величините а и b, зависят от това, в кой квадрант са посочните ъгли на отсечките МА′ и NA′.

23. ИЗЧИСЛЯВАНЕ КООРДИНАТИТЕ НА ПРЕСЕЧНИТЕ ТОЧКИ НА ОСИТЕ С РАМКИТЕ НА ПЛАНОВИТЕ ЛИСТОВЕ

Изчисляването се извършва във формуляра за малките точки, който се подшива към формуляра за изчисляване на осовите точки. Дадени са координатите на осовите точки 1 и 2 (черт. 45), както и тези на рамките на работния кадастрален план, на които лежат точките 1′ и 2′. От тях се изчисляват координатните разлики между 1 и 2, т.е. Δу и Δх и разстоянието 1-2=S. Координатната разлика между 1 и 1′ по оста х или Δх₁ е също известна.

Тогава за точка 1′ имаме: ; подобно за точка 2′: , понеже Δу₂ е известно.

Проверка: ; ; , т.е. изчисляват се страните S1, S2, S3, сборът на които трябва да е равен на общата дължина 1-2 с максимална разлика до 2 см, която се дължи на закръгление при изчисляването. Ако резултатът от проверката е задоволителен, изчисляват се: и .

24. ПОЛУЧАВАНЕ НА ДАННИ ЗА ТРАСИРОВЪЧЕН КАРНЕТ НА ДВОРИЩНА РЕГУЛАЦИЯ

При улици в крива, измерването на абсцисите за трасиране на пресечните точки на дворищните с уличните регулационни линии, се извършва по хордите. Абсцисите се отчитат графически с възможната за мащаба точност и ординатите се изчисляват по следните формули:

а) Изпъкнали криви

, където: у – ордината; R – радиус на кривата осова линия; а – ширина на улицата; R₁ – радиус на регулационната линия ; АВ – хорда, съединяваща две осови точки; х – абсциса, считана от среда-хорда

б) Вдлъбнати криви

, където: у – ордината; а – ширина на улицата; R1 – радиус на кривата регулационна линия ; х – абсциса, считана от среда-хорда; R – радиус на кривата осова линия; АВ – хорда, съединяваща две осови точки.