Приложение 6.2

АНАЛИЗ НА СТАБИЛНОСТТА И НА ПРЕМЕСТВАНИЯТА НА ТОЧКИТЕ

1. Проверката на стабилността на отделната станция и определянето на преместванията й се извършва въз основа на разликите (δr) между измерените в отделните моменти посоки спрямо начално измерените r_i , техните средни грешки μ_δr и m_δr. Определянето на μ_δr и m_δr става по формулите:

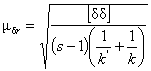
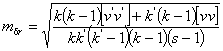
където:

m_δr – е средна грешка, определена от отклонението на измерените посоки от средното аритметично за двата момента

μ_δr - е средна грешка, определена от разликите в измерените посоки в двата момента

v, v^’ – са поправка към посоките в отделните гируси за началния и някой следващ момент на измерване; s – брой на визираните точки, k, k^’ – брой на гирусите в двата момента

; v^p = r (общо средно) – r (ред. ср.)

съответно и за v^’

;

P_δr – тежест на разликата δr

2. Проверката дали станцията е неизменна се извършва чрез проверка на статистическата хипотеза. За целта може да се използува критерия

в който τ_ав е гранична стойност на Фишерово разпределение, а “а” и “в” са съответните степени на свобода брой на μ_δr и m_δr. τ_ав се вземат от съответните статистически таблици, в които се влиза с а, в, α. (Таблица 6.2.1) Когато хипотезата се отхвърля.

3. Станцията може да се счита за стабилна, ако отношението на максималната разлика δr_max в посоките към средната грешка на разликите m_δr е по-малка от τ_α.

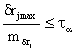
където τ_α е гранична стойност в нормалното разпределение и се взема от статистически таблици за разпределение на максималния член, в който се влиза с вероятност α = 5% и степени на свобода n – 1 (n – брой на точките към които се визира).

4. Опростено може да се приеме, че ако отношението е по-голямо от 1 станцията се е изменила. Като по-строг критерий може да се използува и следният: станцията е стабилна, ако

μ_δr < m_δr

Когато

μ_δr > m_δr

станцията или някоя от точките за ориентиране се е изменила.

5. Редът на работа при идентифициране на стабилните точки е следния: приемат се две точки за изходни. Целесъобразно е те да са разположени и на най-стабилната част от терена, да са максимално отдалечени една от друга и по възможност по-далече от изследвания обект.

Пример 6.2.1.

В двата момента на измерване е визирано към n = 6 посоки и са получени средни грешки на измерена посока, както следва:

m_r = 4,14^cc m_δr = 5,64

m_r′ = 3,84 μ_δr′ = 3,30

Степените на свобода са: а = n – 1 = 5 и

в = n – 1 + n – 1 = 10

При α = 5%

τ_5,5,10 = 4,74

В случая

Следователно станцията може да се счита за стабилна.

Пример 6.2.2.

Визирано е към n = 7 посоки

при δr = 15,60, m_δr = 5,64 и

при α = 5%, т.е. P = 95% от таблицата се взема

τ_pn = 2,386

или

Следователно станцията се е изменила.

6. Преместванията на тези точки се приемат за нули в уравненията на наблюденията. Съставят се и се решават нормалните уравнения, в резултат на което се получават компонентите на преместванията на останалите n – 2 точки от мрежата, средната грешка за единица тежест и на търсените премествания.

7. Ако приетите за база две точки са запазили действително своето първоначално положение, изчислените премествания на останалите точки, които не са променили първоначалното си положение, трябва да се получат равни на нула или да се отдалечават от нея само в границите на влиянието на случайните грешки.

8. При положение, че една или двете точки от изходната база са се преместили между двата момента на наблюдение, за стабилните точки от мрежата ще се получат премествания отлични от нула, която както и преместванията на останалите нестабилни точки, ще съдържат влиянието на завъртането, преместването и изменението на дължината на приетата страна за база.

9. Приемат се последователно за неизменни бази отделните триангулачни страни, респективно нивелачни репери или всички комбинации между триангулачните точки (по двойки) – нивелачните репери и последователно се извършва изравнение на мрежата.

10. Получените премествания и средните им грешки на отделните точки се разглеждат като статистически редове. Отбелязаното в точка 6 свойство ще се използува тук като се изследва разпределението на максималния член на статистическия ред, т.е. отклонението на максималния член от нула. За целта се проверява критерия представляващ отношение на максималния член δx_max към средната му грешка m_δx дали е по-голямо или равно на граничната стойност τ_αq на разпределението на максималния член, т.е. проверява се нулевата хипотеза.

При вероятност α = 5% и q равно на броя на определените премествания на дадена точка (равна на броя на приетите бази, от които са определени) се получава τ_αq от статистическите таблици за разпределение на максималния член дадени в книгите по статистика (таблица 6.2.2).

11. Ако хипотезата се потвърди, т.е. δx_max е по-малко от τ_αq m_δx се приеме, че в разглежданата точка и приетата база не са настъпили изменения, т.е. те са стабилни. Ако се отхвърли, това означава, че има настъпило преместване и се проверява за следващия по големина член от реда.

12. Точките, при които нулевата хипотеза се приема за двата реда δx δy заедно с точките, приети за база на съответното изравнение, могат да се считат за стабилни, а преместванията на останалите точки определени при това изравнение за действителни.

13. За изследване на преместванията на точките от изследвания обект се дефинира нулева хипотеза

което означава, че вероятността (при нормални условия на измерване и липса на преместване) да се появят премествания δx_max които да са по-големи от произведението на граничната стойност τ_αw-1 или τ_αn на разпределение със средна квадратна грешка в определяне на преместванията при дадени условия (степени на свобода w – 1 и ниво на значимост α) е много малка (напр. 5%). При положение, че такова отклонение се появи, това означава, че в точките и изследвания обект са настъпили деформации и нулевата хипотеза следва да се отхвърли. Стойността на τ_αn и τ_αw-1 да се определя от статистически таблици (таблица 6.2.2) за разпределение в случая на максималния член, с който се влиза в броя на преместванията (напр. по ос X за дадена точка и нивото на значимост α равно обикновено на 5% или p – α = 95%).

14. Когато се изследват едновременно преместванията на всички n точки от изследвания обект, получени от изравнението на разликите на наблюденията, преместванията образуват статистически ред. Хипотезата при отхвърлянето й за максималния член се проверява последователно за всички премествания (точки) от реда (изследвания обект). По този начин се установяват точките, които са останали стабилни и тези, които са се преместили.

15. Редът на работа при установяване на стабилните репери е следният:

Приемат се последователно за изходни началните коти на отделните репери и чрез изравнените превишения в дадения цикъл (W) се определят котите на останалите репери.

Образуват се последователно разликите ΔH_i между така определените коти и котите определени при изходното (първоначалното) измерване.

Проверява се нулевата хипотеза

т.е. възможността (при нормални условия) да се появят разлики ΔH които да са по-големи от произведението на граничната стойност на нормалното разпределение τ_α с дадената квадратна грешка в определянето на превишенията при дадените условия (степента на свобода и ниво на значимост α (напр. 5%) е много малка.

Репери, за които разликите ΔH_i са по-малки от произведението τ_αm_δh се приемат за стабилни заедно с изходните при съответното изчисление (цикъл).

Стойността на m_δh се изчислява по

или

където:

μ_k – е средната грешка на километър двойно пронивелирано разстояние, равна за нивелация І клас на 0,4 mm и за нивелация ІІ клас – 0,8 mm

μ_cm = 0,06 – 0,15 (средно 0,10 mm за нивелация І кл.) ср. кв. грешка на една станция при разстояние на визиране около 20 m

D – разстояние между реперите в km

n – брой на станциите до проверявания репер

τ_α = 1,96 при ниво на значимост α = 5%. за други нива α да се използуват съответни статистически таблици.